The binary search algorithm is very effective, as each iteration reduced the number of items to search by one-half. However, since data is stored in an array, insertions and deletions are not efficient. Binary search trees store data in nodes that are linked in a tree-like fashion. For randomly inserted data, search time is O(lg n). Worst-case behavior occurs when ordered data is inserted. In this case the search time is O(n).

Theory

     Each node of a Binary Search Tree (BST) stores a piece of data, called the key. Each node has below it a left subtree and a right subtree. The topmost node is called the root and a node with no subtrees is called a leaf.

     A binary search tree is a tree where each node has a left and right child. Either child, or both children, may be missing. Figure 3-2 illustrates a binary search tree. Assuming k represents the value of a given node, then a binary search tree also has the following property: all children to the left of the node have values smaller than k, and all children to the right of the node have values larger than k. The top of a tree is known as the root, and the exposed nodes at the bottom are known as leaves. In Figure 3-2, the root is node 20 and the leaves are nodes 4, 16, 37, and 43. The height of a tree is the length of the longest path from root to leaf. For this example the tree height is 2.

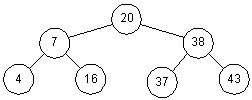
Figure 3-2: A Binary Search Tree

     To search a tree for a given value, we start at the root and work down. For example, to search for 16, we first note that 16 < 20 and we traverse to the left child. The second comparison finds that 16 > 7, so we traverse to the right child. On the third comparison, we succeed.

     Each comparison results in reducing the number of items to inspect by one-half. In this respect, the algorithm is similar to a binary search on an array. However, this is true only if the tree is balanced. For example, Figure 3-3 shows another tree containing the same values. While it is a binary search tree, its behavior is more like that of a linked list, with search time increasing proportional to the number of elements stored.


Figure 3-3: An Unbalanced Binary Search Tree

Insertion and Deletion

     Let us examine insertions in a binary search tree to determine the conditions that can cause an unbalanced tree. To insert an 18 in the tree in Figure 3-2, we first search for that number. This causes us to arrive at node 16 with nowhere to go. Since 18 > 16, we simply add node 18 to the right child of node 16 (Figure 3-4).

     Now we can see how an unbalanced tree can occur. If the data is presented in an ascending sequence, each node will be added to the right of the previous node. This will create one long chain, or linked list. However, if data is presented for insertion in a random order, then a more balanced tree is possible.

     Deletions are similar, but require that the binary search tree property be maintained. For example, if node 20 in Figure 3-4 is removed, it must be replaced by node 37. This results in the tree shown in Figure 3-5. The rationale for this choice is as follows. The successor for node 20 must be chosen such that all nodes to the right are larger. Therefore we need to select the smallest valued node to the right of node 20. To make the selection, chain once to the right (node 38), and then chain to the left until the last node is found (node 37). This is the successor for node 20.


Figure 3-4: Binary Tree After Adding Node 18


Figure 3-5: Binary Tree After Deleting Node 20 

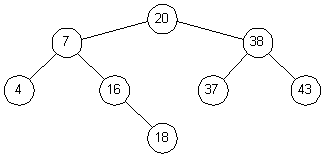
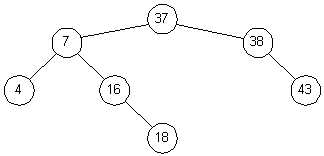
B-Tree algorithm:

Recursive

Insert value in tree
    Insert value in subtree starting at root node
    if root node split,
        Create new root node with middle value, left child points to left
            split node and child after middle value is right split node.

Insert value into subtree starting at node T:
    if T is a leaf node,
        Insert value into node T (no children)
    else
        if value < first key in T then
            Insert value into subtree starting at left child
        else
            Find first key such that value < key
            Insert value into subtree starting at child immediately after key

        if child node split,
            Insert its middle value into node T after key
            (Key's pointer points to left split node
             Middle value's pointer points to right split node)

Insert value into node T:
    if node T is full,
        split into left node < middle value
        and right node > middle value
        if value < middle value,
            Insert value into left node
        else
            Insert value into right node.

Delete value from tree:
    Search root of tree for first key >= value
    if key = value then
        if root is a leaf then
            Remove key from root
        else
            if left child of key is fuller than right child then
                Delete Immediate Predecessor of key
            else
                Delete Immediate Successor of key
            Replace key with deleted key from previous operation
            If child node is < 1/2 full then
                if neighbor is > 1/2 full then
                    rotate first or last key of neighbor (depending on
                    direction of move) into root to replace key between
                    the child and the neighboring sibling and move that key
                    into the child node
                else
                    join child with neighboring sibling
                    Remove key between them from root
                    Insert key between them into node resulting from the join
                    if number of keys in root = 0, replace root with only
                        remaining child.
    else
        Delete value from subtree before key
            (or right subtree if no keys are > value)
        if subtree < 1/2 full then
            ... same procedure as above


Delete immediate predecessor of key:
    Delete rightmost value of left child (before) key, returning that value
    if left child < 1/2 full then
        ... same as above

Delete rightmost value of tree:
    if tree root is not leaf (subtree is taller than one level), then
        Delete rightmost value of right child of root (pointer after last key)
        if right child of root < 1/2 full then
            ... same as above
    else
        Remember rightmost key and delete it from "root" of subtree.
btree.cpp
btree.h
Professional C++ Implementation